ورقة عمل درس التوزيع الطبيعي الرياضيات للصف 12 عام
محتوى الموضوع
هدا الملف ل الصف 12 عام لمادة رياضيات ثاني عشر عام فصل ثالث
ورقة عمل درس التوزيع الطبيعي الرياضيات للصف 12 عام
في هذا الدرس سوف أتعلم :
1 – إيجاد المساحة المحصورة تحت منحنيات التوزيع.
2 – إيجاد احتمالات التوزيعات الطبيعية ، و إيجاد قيم البيانات عند إعطاء الاحتمالات.
_ يسمى التوزيع الاحتمالي لمتغير متصل بالتوزيع الاحتمالي المتصل ، يسمى التوزيع الاحتمالي المتصل الأكثر استخداماً بالتوزيع الطبيعي
_ تكون خواص التوزيع الطبيعي كما يلي :
– يتسم التمثيل البياني للمنحنى بأنه متصل و يشبه شكل الجرس و متماثل بالنسبة للوسط.
– يتسم الوسط و الوسيط و المنوال بالمساواة و المركزية.
– يعد المنحنى متصلاً
– يقترب المنحنى من المحور الأفقي X و لكنه لا يتلامس معه أبداً
– المساحة الكلية تحت المنحنى تساوي 1 أو % 100
_ بزيادة حجم العينة و الحد من عرض الفئة ، يصبح التوزيع أكثر و أكثر تماثلاً ، فإن كان من الممكن اعتيان المجتمع الإحصائي بأكمله ، فإن التوزيع سيقارب التوزيع الطبيعي كما هو موضح.

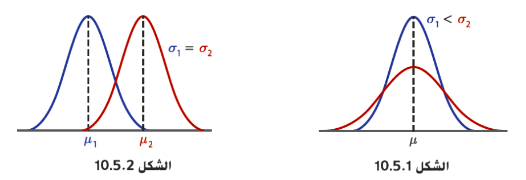
_ لكل متغير عشوائي ذي توزيع طبيعي ، يعتمد شكل منحنى التوزيع الطبيعي و موقعه على المتوسط و الانحراف المعياري ، فعلى سبيل المثال ، يمكنك أن ترى في المثال 10,5,1 أن زيادة حجم الانحراف المعياري تزيد من تسطح المنحنى ، و يؤدي التغير في المتوسط ، كما يوضح الشكل 10,5,2 ، إلى إزاحة أفقية للمنحنى.
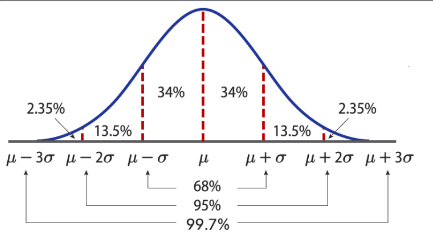
_ تمثل المنطقة الواقعة تحت منحنى التوزيع الطبيعي بين قيمتين للبيانات النسبة المئوية من البيانات الواقعة داخل هذه الفترة ، يمكن استخدام القاعدة التجريبية لوصف المساحة تحت المنحنى الطبيعي و ضمن فترات تبعد انحرافاً معيارياً واحداً أو اثنين أو ثلاثة عن الوسط.
– القاعدة التجريبية :
_ في التوزيع الطبيعي ذي الوسط 4 و الانحراف المعياري 0 ، ينطبق ما يلي :
– تقع تقريباً % 68 من قيم البيانات فيما بين
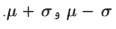
– تقع % 95 من البيانات بين

– تقع % 99,7 من قيم البيانات بين

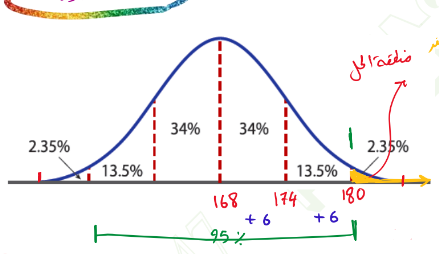
_ الارتفاع يتوزع طول 880 طالباً بمدرسة الشرق الثانوية طبيعياً بوسط 168cm و انحراف معياري 6cm
أ – كم عدد الطلاب الذين يزيد طولهم عن 180cm تقريباً ؟
– أولاً / نحدد المنطقة التي تريد عند 180cm باللون الأصفر
– ثانياً / نحسب نسبة هذه المنطقة
– المنطقة التي عليها خط أخضر في الرسم نسبتها % 95 ، إذا نسبه مساحة الذيلين يمين و يسار % 5 ، نسبة الذيل الأيمن فقط و هي منطقة الحل % 2,3
– ثالثا / نحسب عدد الطلاب :
طالب 22 = ( 880 ) % 2,5 = عدد الطلاب فوق 180cm
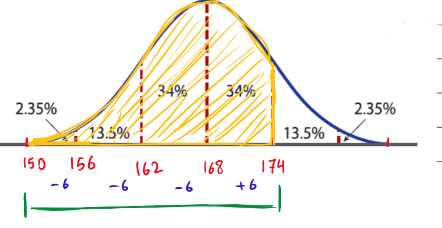
ب – ما النسبة المئوية للطلاب الذين يتراوح طولهم بين 150cm و 174cm ؟
– أولاً / نحدد المنطقة بين 150 ، 174
– ثانياً / نحسب نسبة مساحة هذه المنطقة ( باللون الأصفر )
% 2,35 + % 13,5 + % 34 + % 34 = النسبة
% 84 = % 83,85 =
إذا % 84 من الطلاب تقريبا تتراوح أطوالهم بين 150cm و 174cm
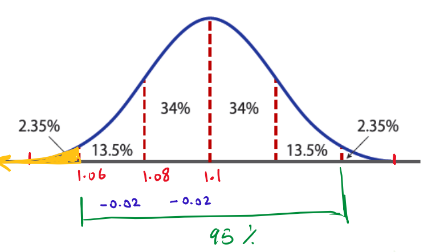
_ الصنيع : توزع آلة لتعبئة قوارير الماء كميات مختلفة قليلا من الماء في كل قارورة ، افترض أن حجم الماء في 120 قارورة له توزيع طبيعي وسطه 1,1L و انحراف معياري يساوي 0,02L
أ – ما العدد التقريبي لقوارير الماء التي تملأ بكمية أقل من 1,06L ؟
– أولاً / نحدد المنطقة الأقل من 1,06 ( اللون الأصفر )
– ثانياً / نحسب نسبة مساحة هذه المنطقة
المنطقة المحددة بالأخضر % 95 ، إذا نسبة الذيلين % 5 ، و نسبة الذيل الأيسر = % 2,5
– ثالثا / توجد عدد القواريد في تلك المنطقة
قواريد 3 = ( 120 ) % 2,5 =
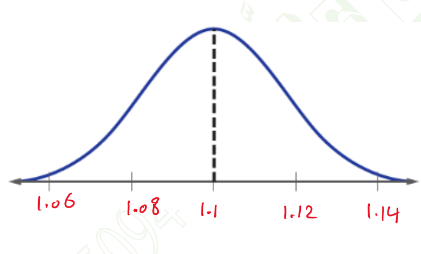
ب – ما النسبة المئوية من القوارير التي تضم ما بين 1,08L و 1,14L ؟
– أولاً / نحدد المنطقة ( باللون الأصفر )
– ثانياً / نحسب المساحة لهذه المنطقة
% 13,5 + % 34 + % 34 = النسبة
% 81,5 =
إذا % 81,5 من القواريد تضم ما بين 1,08L و 1,14L
_ إيجاد قيم z
– في حين يمكن استخدام القاعدة التجريبية في تحليل التوزيع الطبيعي ، تكون فائدتها الوحيدة عند تقييم قيم محددة ، مثل μ + σ ، يمكن تحويل المتغير الذي يتم توزيعه طبيعياً إلى قيمة معيارية أو قيمة z ، حيث يمكن استخدامه في تحليل أي مدى من القيم في التوزيع الطبيعي ، يعرف هذا التحويل بالمعيارية ، تعرف قيمة z أيضاً بالدرجة z و إحصاء اختبار z ، و تمثل عدد الانحرافات المعيارية التي تشكلها قيمة بيانات معينة من الوسط.
_ المفهوم الأساسي صيغة قيم z
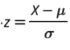
– قيم z الخاصة بقيمة البيانات في مجموعة بيانات محددة من خلال ، حيث x هي قيم البيانات ، و μ هو الوسط ، و σ هو الانحراف المعياري
_ جد كلاً مما يلي :
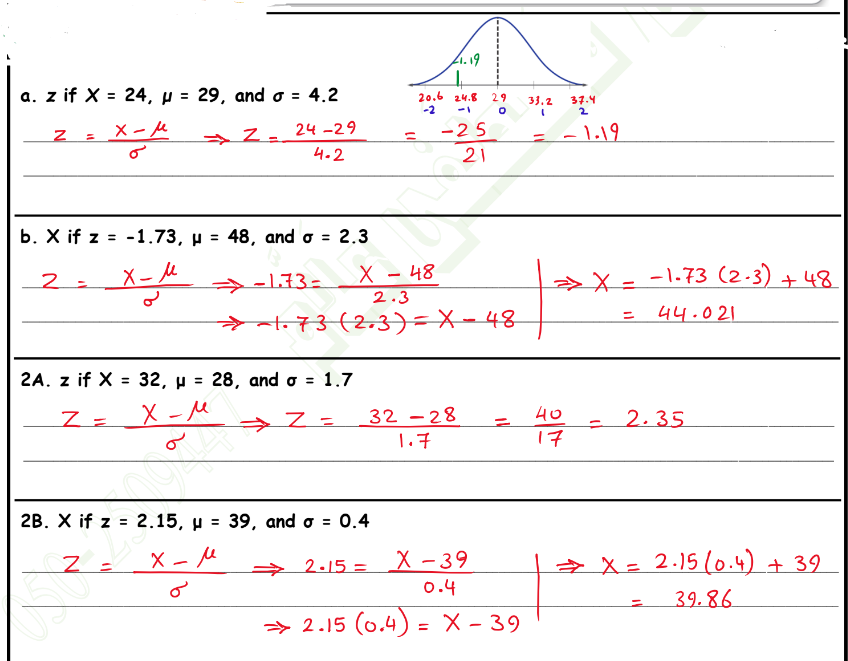
_ استخدام التوزيع المعياري :
– يحتوي كل متغير عشوائي تم توزيعه طبيعياً على وسط و انحراف معياري فريدين ،و هو ما يؤثر على شكل و موقع المنحنى ، و نتيجة ذلك ، يوجد العديد من التوزيعات الاحتمال الطبيعية اللانهائية ، و لحسن الحظ ، يمكن ربطهم جميعاً بتوزيع واحد يسمى التوزيع الطبيعي المعياري ،
التوزيع الطبيعي المعياري هو توزيع طبيعي لقيم z بمتوسط 0 و انحراف معياري 1.
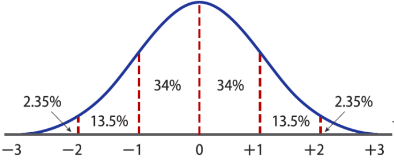
_ المفهوم الأساسي خواص التوزيع الطبيعي المعياري
– المساحة الكلية تحت المنحنى تساوي 1 أو % 100
– تقع المنطقة كلها بين 3 – = z و 3 = z
– التوزيع متماثل
– الوسط يساوي 0 و الانحراف المعياري يساوي 1
– يقترب المنحنى من المحور الأفقي X و لكنه لا يتلامس معه أبداً
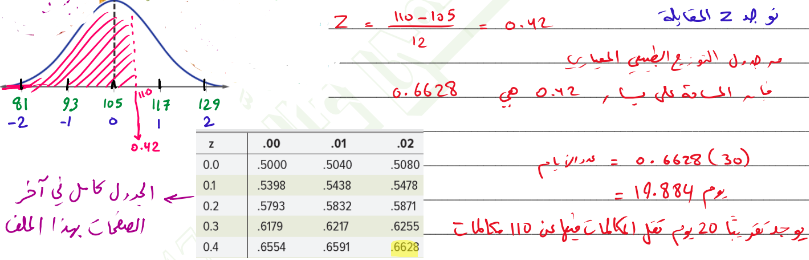
_ الاتصالات بلغ متوسط المكالمات التي يستقبلها مندوب خدمة العملاء كل يوم خلال شهر 30 يوماً 105 مكاملات بالانحراف المعياري 12 ، جد عدد الأيام التي تقل المكالمات فيها عن 110 مكالمات ، افترض أن عدد المكالمات يتم توزيعه طبيعياً
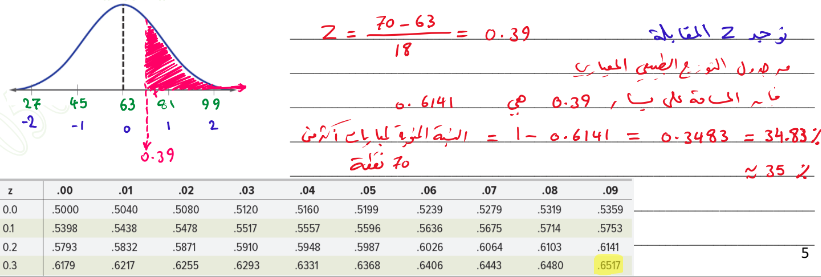
_ كرة السلة بلغ متوسط عدد النقاط التي أحرزها أحد فرق كرة السلة خلال موسم واحد 63 مع انحراف معياري 18 ، إذا كانت هناك 15 مباراة خلال الموسم ، فجد النسبة المئوية للمباريات التي أحرز فيها الفريق أكثر من 70 نقطة ، افترض أن توزيع عدد النقاط كان طبيعياً
_ إيجاد قيم z التي تتطابق مع منطقة معينة
– جد فترة قيم z المرتبطة بكل منطقة
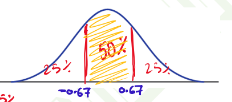
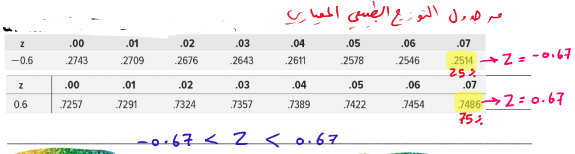
أ – النسبة الوسطى % 50 من البيانات.
ب – النسبة الخارجية % 20 من البيانات

أ – نسبة % 25 الوسطى من البيانات

ب – النسبة الخارجية % 60 من البيانات

_ إيجاد الاحتمالات في التوزيع الطبيعي
– الأرصاد الجوية يتم توزيع درجات الحرارة لأحد الشهور في إحدى مدن دولة الإمارات حيث درجة 81 = μ و درجة 6 = σ ، جد كل احتمال ، و استخدم حاسبة التمثيل البياني لرسم المنطقة المقابلة الواقعة تحت المنحنى.
أ –
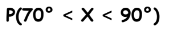

ب –
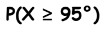

_ الاختبار توزع درجات اختبار معياري توزيعاً طبيعياً فيه 72 = μ و 11 = σ ، جد كل احتمال مما يلي و استخدم حاسبة التمثيل البياني أو الجداول لإيجاد المساحة تحت المنحنى
أ –


ب –
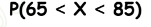

_ من الحياة اليومية إيجاد فترات البيانات
– الدراسة الجامعية تتوزع درجات اختبار قبول الجامعة في قسم الرياضيات طبيعياً حيث 65 = μ و 8 = σ
أ – إذا أرادت فاطمة أن تكون ضمن ال % 20 الأوائل ، فما الدرجة التي يجب عليها تحقيقها ؟

ب – تتوقع فاطمة أن تحصل على درجة ضمن النسبة الوسطى % 90 في التوزيع ، فما مدى الدرجات الذي يقع ضمن هذه الفئة ؟

_ البحث يختار باحث خلال إحدى الدراسات الطيبة مجموعة للدراسة وسط وزنها 86Kg و انحرافها المعياري 5,5Kg ، افترض أن الأوزان موزعة طبيعياً ،
أ – إذا كانت الدراسة ستركز بصورة رئيسة على المشاركين الذين تقع أوزانهم في النسبة الوسطى % 80 من مجموعة البيانات ، فما مدى الأوزان الذي سيضمنه ذلك ؟

ب – إذا تم الاتصال بالمشاركين الذين تقع أوزانهم في النسبة الخارجية % 5 من التوزيع بعد أسبوعين من الدراسة ، فما مدى أوزان الأشخاص الذين سيجري الاتصال بهم ؟

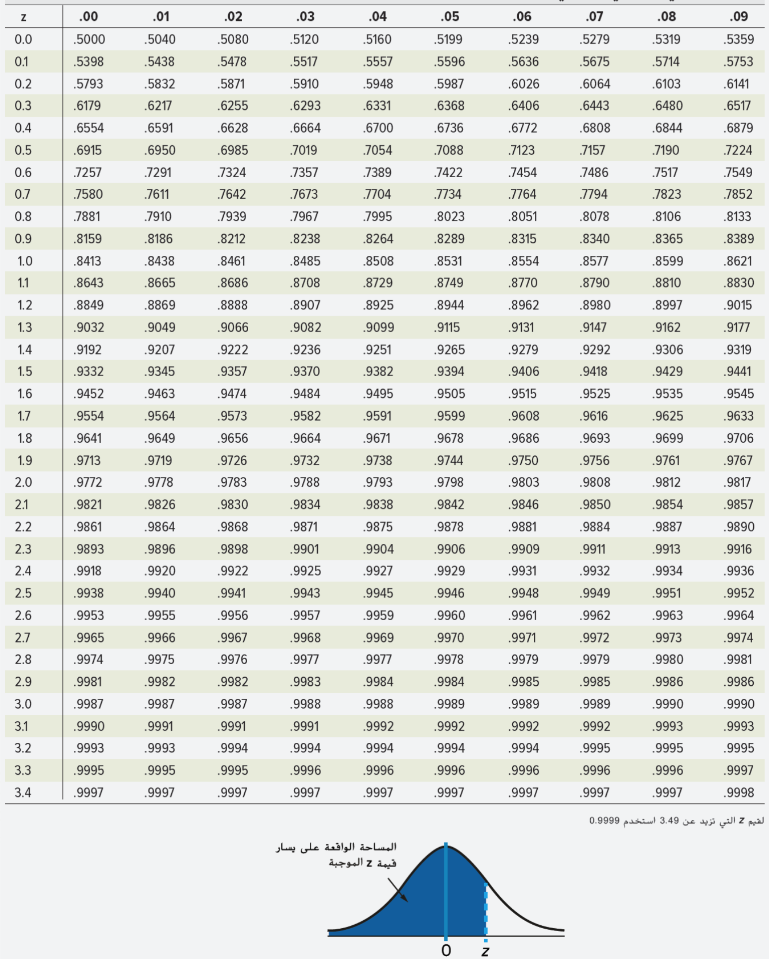
_ الجدول أ التوزيع الطبيعي المعياري
– التوزيع الطبيعي المعياري التراكمي
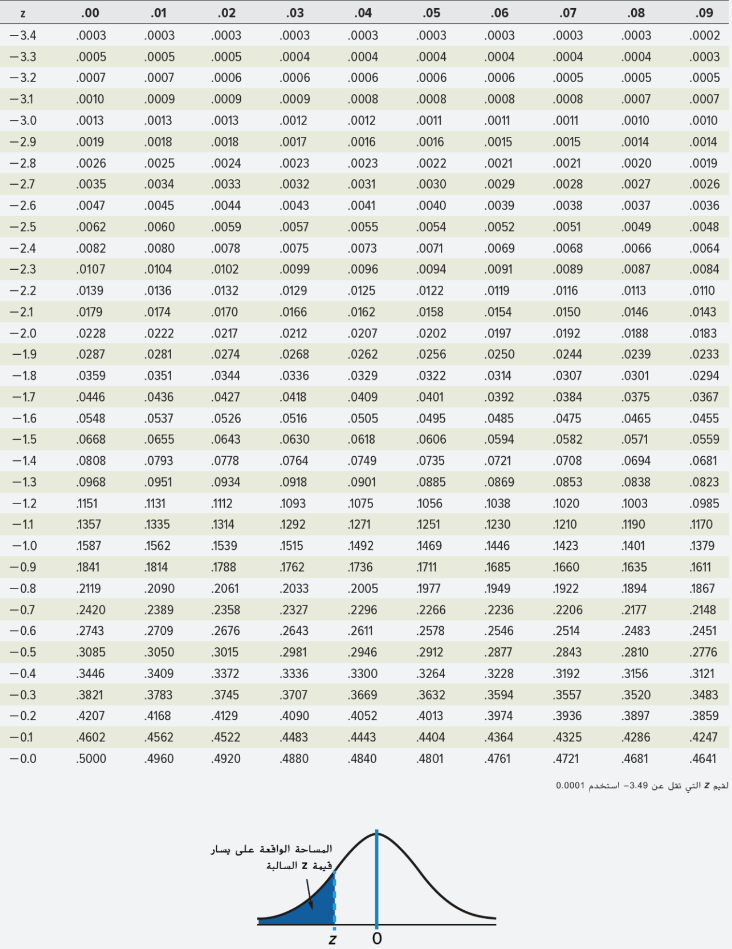
_ الجدول أ ( التابع )
– التوزيع الطبيعي المعياري التراكمي